Syntax-Tree Queries
by Fabian Yamaguchi
In this article, we introduce readers to syntax-tree queries and show how they can be used as a computationally cheap approach for identifying code that handles attacker-controlled input or follows known bad practices. On the one hand, this article provides a practical introduction to mining code for patterns in its abstract syntax trees via a fluent query language. On the other hand, we discuss the limitations of syntax-tree queries at length.
If you find that the terminology used in this article is foreign to you, we hope that our article on Code Property Graphs can help you out.
What are Abstract Syntax Trees?
Throughout this article, we are using variations of the following small sample code snippet taken (taken from this paper):
val code = """
void foo () {
int x = source();
if(x < MAX) {
int y = 2*x;
sink(y);
}
}
"""
The snippet consists of a single function named foo without a return
value. It calls a function called source on line 2 and stores its
result in an integer called x. A subsequent check on line 3
determines whether x is smaller than a constant MAX, and if so, the
value of 2*x is stored in y on line 4 and passed as an argument to the
function sink on line 5.
We can import this code snippet directly on the Ocular shell (see top level commands).
importCode.c.fromString(code)
Once imported, we can plot the abstract syntax tree of foo to get a
first idea of what an abstract syntax tree is.
cpg.method.name("foo").plotDotAst
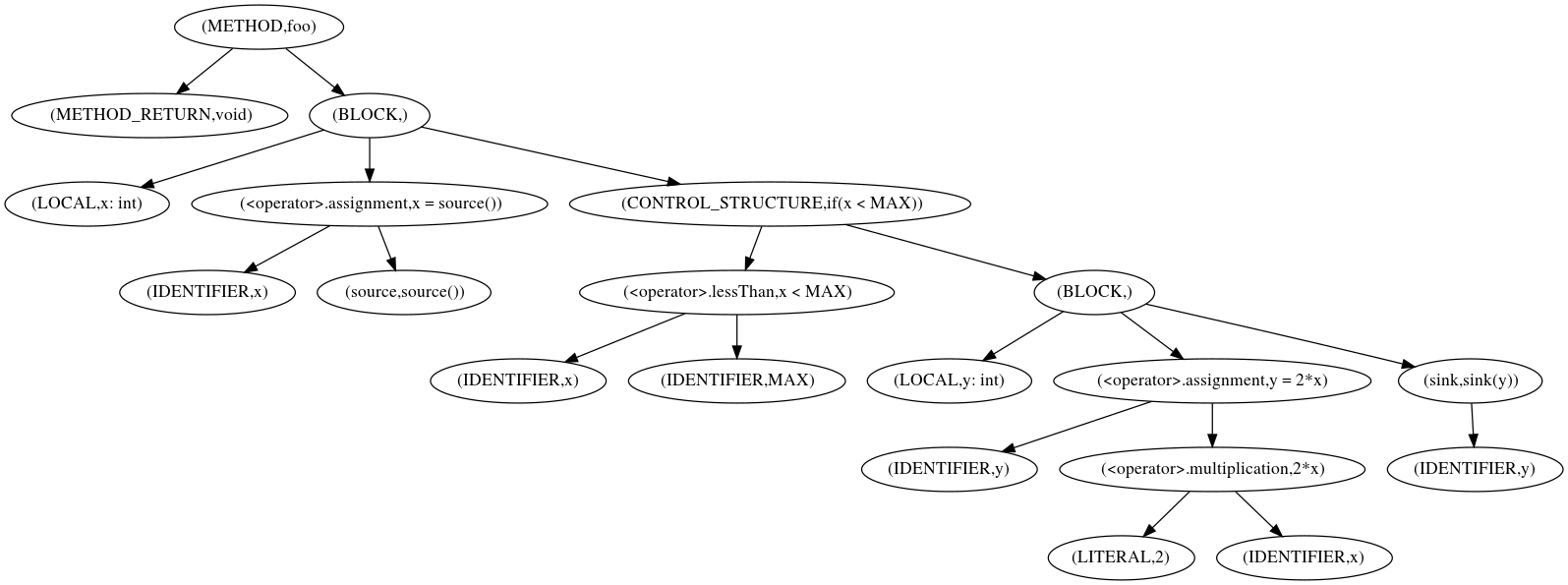
As shown in the sample plot in Figure 1, an abstract syntax tree is a tree-like structure that makes the decomposition of code into its language constructs explicit. The tree consists of nodes and edges visualized in the plot as ellipses and arrows respectively.
Nodes represent language constructs such as methods, variables, and
control structures, while edges indicate decomposition. For example,
at the very top of the tree, we see a node representing the entire
function foo, and directly beneath it, we see a node for the return
type void and one for the function body, denoted as a BLOCK. The
edges between the function- and the two other nodes indicates that the
function can be decomposed into a return type and a block of code, and
outgoing edges from BLOCK show that this block of code can be
further decomposed.
In the plot, the pair (type,attribute) is displayed in each node,
where type is the node type and attribute is one of the values
that is particularly indicative for the node, e.g., the method name
for method nodes. We make an exception for calls, where we display the
pair (name,attribute).
Basic AST Traversals
The most basic traversal that you can
execute on any AST node is ast, which traverses to all nodes of the
AST rooted in the node. For example,
cpg.method("foo").ast.l
gives you all AST nodes of the AST for the method foo. As each AST
node is also the root of a subtree, you can also think of this
operation as an enumeration of all subtrees. These can be filtered by
type. For example,
cpg.method("foo").ast.isCall.code.l
gives you all outgoing calls from foo while
cpg.method("foo").ast.isControlStructure.code.l
gives you all control structures. For method nodes, we also offer shorthands for the most common node types. Using these shorthands, the two queries can be written as
cpg.method("foo").call.code.l
and
cpg.method("foo).controlStructure.code.l
respectively.
It is also possible to walk the tree upwards using inAst or
inAstMinusLeaf where the latter excludes the start node. In our
running example, consider for example the situation where it is known
that calls to source return values that an attacker can
influence.
cpg.call.name("source").inAstMinusLeaf.isCall.name(".*assignment.*").argument(1).l
The query begins by selecting all calls to source, encoded in the
graph as nodes of type CALL with a string property called name
that is set to "source". From there, we walk edges backwards
until we reach the method node using inAstMinusLeaf. For the set of
nodes thus collected, we determine only those which are calls
(isCall) to the assignment operator .name(".*assignment.*"). For
each of these, we determine their first argument, the assignment
target.
As certain operators exist across programming languages and operating on them via AST-queries is common, we have created a decorator language to simplify these queries. In practice, we would write the following query that is equivalent to the former query.
cpg.call("source").inAssignment.target.l
Control Structures
Abstract syntax trees include control structures such as if-,
while or for-statements. Our example program contains only a
single control structure, namely, the if-statement on line 3.
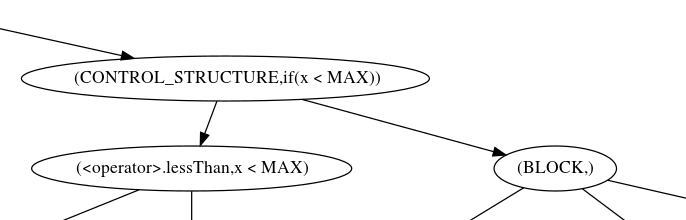
Figure 3 shows how if-statements are represented in the syntax
tree. The tree consists of two sub trees, one that holds the condition
x < MAX and another that holds the statements in the
if-block. Conditions can be selected as follows:
cpg.method("foo").controlStructure.condition.code.l
=> List("x < MAX")
The body of the if-statement can be selected using whenTrue:
cpg.method("foo").controlStructure.whenTrue.l
res16: List[AstNode] = List(
Block(
id -> 17L,
code -> "",
order -> 2,
argumentIndex -> 2,
typeFullName -> "void",
dynamicTypeHintFullName -> List(),
lineNumber -> Some(5),
columnNumber -> Some(4),
depthFirstOrder -> None,
internalFlags -> None
)
)
For if-else constructs, whenFalse returns the else block, however,
since no else block exists in our example, an empty list is
returned:
cpg.method("foo").controlStructure.whenFalse.l
=> List[AstNode] = List()
As each of the nodes returned by .ast are also roots of syntax
trees, we can identify nested structures by chaining basic
operations.
cpg.method("foo").controlStructure.whenTrue.ast.isCall.code.l
=> List[String] = List("y = 2*x", "sink(y)", "2*x")
yields all calls nested inside if blocks. You may ask yourself why
2*x is returned as a call. The reason is that we model all
invocations of built-in operators as calls to methods with the name
<operator>.$operatorName, where $operatorName may for example be
"multiplication", or "assignment".
One example scenario where control structure access comes in handy is
when you wish to determine all methods that call a specific function
but do not include a necessary check. Say, for example, that we want
to identify functions that call source but they do not include a
check against MAX. The following query achieves this:
cpg.method.filterNot(_.controlStructure(".*MAX.*"))
.filter(_.callee.name(".*source.*")).l
=> List()
Note, however, that the query does not specify the order in which these statements must occur, e.g., the check may happen too late. Control flow graphs and dominator trees are the right tools to reason about statement order. These structures are available in the code property graph as well, but we do not discuss them in this article.
Nesting of control structures
Let us modify our example code slightly as follows to obtain a deeper understanding of what one can and cannot do using the control structures exposed by abstract syntax trees.
val code = """
void foo () {
int x = source();
if (x > 10) {
goto end;
}
while(x++ < MAX) {
if(x != 0) {
int y = 2*x;
sink(y);
}
}
end:
}
"""
Importing and plotting yields the following:
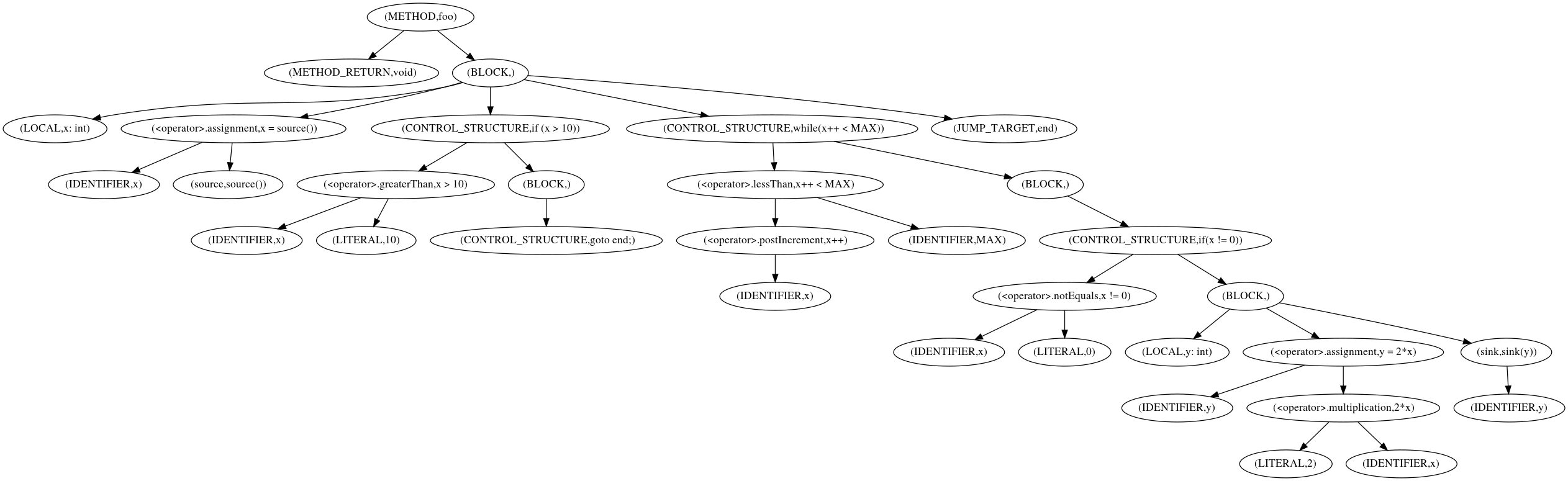
As we can see in Figure 4, the language formulated so far can be used
easily to describe nested constructs. For example, if we would like to
identify all calls to sink nested in an if-block that is itself
nested in a while block, we could use the following query:
cpg.call("sink")
.inAst.filter(_.isControlStructure.code("if.*"))
.inAst.filter(_.isControlStructure.code("while.*")).l
=> List[AstNode] = List(
ControlStructure(
id -> 19L,
code -> "while(x++ < MAX)",
columnNumber -> Some(2),
lineNumber -> Some(9),
order -> 3,
parserTypeName -> "WhileStatement",
argumentIndex -> 3,
depthFirstOrder -> None,
internalFlags -> None
)
)
Alternatively, we can walk the tree from its top to achieve the same:
cpg.method
.controlStructure("while.*")
.ast.isControlStructure.code("if.*")
.ast.isCallTo("sink").l
=> List[Call] = List(
Call(
id -> 36L,
code -> "sink(y)",
name -> "sink",
order -> 2,
methodInstFullName -> None,
methodFullName -> "sink",
argumentIndex -> 2,
dispatchType -> "STATIC_DISPATCH",
signature -> "TODO assignment signature",
typeFullName -> "ANY",
dynamicTypeHintFullName -> List(),
lineNumber -> Some(12),
columnNumber -> Some(0),
resolved -> None,
depthFirstOrder -> None,
internalFlags -> None
)
)
While the syntax tree is not primarily concerned with exposing control
flow, when a function only contains structured control structures such
as if blocks or while loops, limited reasoning about control flow
is possible. For example, since the call to sink is nested inside
the if block and while loop, we can be certain that the conditions
introduced by these two control structures are evaluated at least once
before sink is called. We can also be certain that a sibling tree to
the left is executed before a tree itself.
This, however, does not work in the face of unstructured control flow
as introduced by goto. We make these statements as well as their
jump targets visible in the tree, however, allowing functions where
control flow must be analyzed with control flow graphs can be
determined.